前回の記事「自己対戦及び連続対戦の誤差論 1:標準誤差と信頼区間」では、自己対戦/連続対戦の対局数が十分に大きい場合に誤差をどのように見積もればいいのかを整理しました。今回は、対局数の影響について解説します。
標準誤差は対局数nの平方根に逆比例していました。つまり、対局数が大きくなるほど、誤差は小さくなり、精度が高くなるということになります。
必要な精度というのは、実験者がどれくらいまで求めるのかということに依ってきますが、「実際に誤差を計算してみて、必要な精度が出ているかどうか」というのが「対局数が十分であるかどうか」の基本的な判断基準になります。ただし、誤差の計算には、いくつか注意しなければならないことがあります。それが今回の記事の主題です。
前回の記事で紹介した誤差論は、対局数が多くて標準誤差が小さい時に有効なものでした。そうでない場合には、誤差の見積もりを修正しなければならないことがあります。
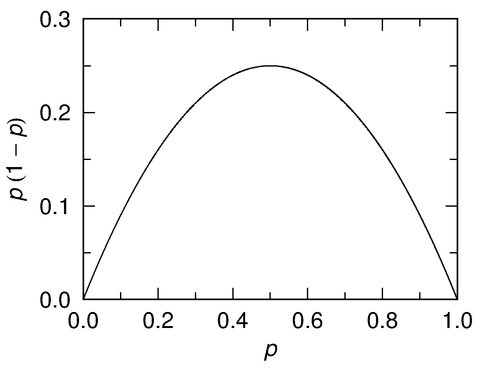
例えば、標準誤差は、勝率の真値pに依存しており、p (1 - p)に比例していました。これは、pの関数として描くと、下図のようになります。
しかしながら、勝率の真値pは分からないため、勝率の推定値qを用いて、標準誤差を推定することになりました。pとqの値が近ければ、この標準誤差の推定は妥当なものとなりますが、もしそうでなければ、標準誤差の推定は的外れなものになってしまうかもしれません。特に、qが0や1に近い場合には、変化が大きいので、注意が必要です。
実際の標準誤差が推定よりも小さい場合には問題はないのですが、推定よりも大きい場合には、実際の精度よりも過剰に精度を見積もってしまうことになるため、問題が生じ得ます。該当する場合には、標準誤差を適度に上方修正して考える必要があるでしょう。
この話は、言い換えると、誤差の高次の項の問題の一種ということになります。誤差が小さければ現れなかった問題が、誤差が大きくなってくると無視できなくなってくるということです(※)。これらの問題をまとめて解決するには、結局のところ、対局数を増やして精度を上げるしかありません。
※(2016年5月31日追記) そもそも「誤差」は真値との差として定義されているわけですが、真値というのは値が分からないものであるため、「誤差」を計算するには真値について何らかの仮定を置く必要があります。これが、誤差論の根本的な問題の一つであり、高次の項の問題の根本もそこにあります。この問題を避けるため、「誤差」という概念は諦めて、「不確かさ」という概念を導入するというのが近年の主流です。「不確かさ」は平均からのばらつきとして定義され、その平均が真値に近いかどうかは問題を切り分けます。「誤差」と異なり、「不確かさ」についてならば、紛れのない国際基準を作ることも可能であり、その国際基準(GUM)は物理学や工学等の分野で広く採用されています。
一方で、誤差の大きさとは直接的に関係無しに、対局数の不足のみによって生じる問題もあります。具体的には、中心極限定理の適用の妥当性の問題です。こちらは理論的に対処することができます。
中心極限定理は、対局数が十分に大きい時に、確率分布が正規分布になることを示していました。しかしながら、実際には、n回連続対戦した時の勝率の推定値qの確率分布は離散確率分布になっており、正規分布のような連続確率分布にはなっていません。なぜなら、qは、自然数である勝ち数kを使って、“k / n”と計算されるからです。もちろん、nが十分に大きくなれば、“k / n”の有理数は実数に近いものとして取り扱うことができるわけですが、実際にそれがどれくらい良い近似であるのかというのは、誤差の評価とは別に、対局数によって決まってくる問題ということになります。
実際の確率分布は、勝率の真値pを用いると、\[\frac{n!}{k! (n - k)!} p^{k} (1 - p)^{n - k},~~ k = n q\]の二項分布として書き表すことができます。
この二項分布の標準偏差は、\[S = \sqrt{\frac{p (1 - p)}{n}}\]であり、前回の正規分布の標準偏差と同じになりますので、標準誤差については、実は対局数に依らずに厳密な値であったということが分かります。
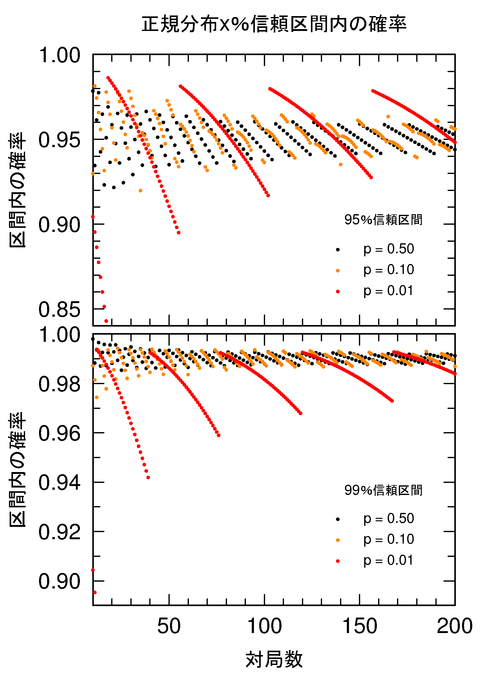
対局数によって変わってくるのは、標準誤差と信頼区間との間の関係です。以下の図は、正規分布において95%信頼区間である「真値±1.96標準誤差」(上図)と99%信頼区間である「真値±2.58標準誤差」(下図)内の実際の確率を表しています。分布が正規分布であれば、それぞれ0.95と0.99になるはずのものですが、実際には二項分布であるために離散的に値が変わってきます。横軸は対局数nです。
二項分布はnが十分に大きければ、正規分布で近似することができます。これは中心極限定理に対応しています。ただし、nが大きくても、n p、もしくはn (1 - p)が小さければ、ポアソン分布になり、正規分布にはなりません。実際に、上記の図でも、pが0.5(黒点)と0.1(橙色点)の時には、正規分布に近い結果になっており、pが0.01(赤点)の時には、正規分布の結果からのズレが大きくなっています。
上の図で示した区間内の確率は大きい分には問題ないのですが、小さくなると、その分だけ信頼が落ちるということになります。また、これらの確率は勝率の真値pに依存しており、真値pは分からないものですので、対局数を調整して信頼を上げるというような操作を行うこともできません。結局のところ、確率の下限の方に着目して、その分だけ信頼区間の%を下方修正して考えるというのが、妥当な解釈ということになるでしょう。
勝率の真値pに対して推定値qを適用してよいということであるのならば、二項分布を用いて、最小の信頼区間を推定することができます。ただし、この信頼区間においても、上で記した「誤差の高次の項の問題」は変わらずに発生し得ます。この処方箋で対処できるのは、「中心極限定理の適用の妥当性の問題」のみです。
さて、前回の記事で、相対レートにおける標準誤差を推定する際に、勝率の標準誤差Sに対する展開を行いました。この展開は、Sがpや(1 - p)よりも十分に小さい時には有効なのですが、そうでない場合には使うことができません。特に、勝率に対してそれなりに広い信頼区間が与えられた時には、破綻してしまいます。
この問題も「誤差の高次の項の問題」の一種ですが、これは観測データの直接的な処理の問題ではなく、誤差伝播という間接的な処理の問題であるため、理論的な対処が可能です。
実際に、相対レートは勝率に対して単調増加関数ですので、信頼区間が与えられた時には、展開を用いなくても、上限値と下限値をそのまま放り込むことで、対応する相対レートの信頼区間を得ることができます。
これらの信頼区間の見積もりはコンピュータで簡単に計算することができます。「連続対戦における信頼区間の計算」の資料記事に計算プログラムを記しました。
以上、自己対戦/連続対戦の結果から勝率やレートを推定する際の誤差論について整理しました。結局のところ、実験の精度はデータの質と量で決まってきます。地道にデータを収集する基礎研究が華々しい成果の基盤になるのだと思います。

コメント