通常、対局結果は時系列のデータリストとして記録されます。「いついつにAがBに勝った」というようなデータが逐次的に記録されていくわけです(※大会等では「第1回戦の記録」というような同時刻扱いのデータも出てきます)。
この対局結果のデータリストから棋力を推測しようというのがイロレーティングの理論でした。イロレーティングについては以下の記事をご参照ください。
イロレーティングでは、逐次的に勝者のレートを上げ、敗者のレートを下げることで均衡点を探すということをします。対局数が少ない時にはレートを適切に測ることはできませんが、対局数が多ければ、レートは均衡点の周りを一定の標準偏差で揺れ動くことになります。
この手法は簡単でありながら、時系列のデータにも自然に対応しており、棋力のなだらかな変化も均衡点の推移として反映することができるという優れた手法です。その一方で、均衡点をどのように見積もればいいのかが明確ではないこと、均衡点の見積もりに多数のデータが必要であり、また不確かさの評価が明確ではないこと、レート上限/下限の境界付近において偏りが発生すること等の問題点もあります。
ベイズ統計を用いると、いくつかの仮定の下で、もう少し洗練された手法に改良することができますが、同時に、仕組みが複雑になってしまいます。この手法の洗練さ(信頼性とはまた別)と簡単さとのトレードオフは悩ましいところです。結局のところ、データの量が限られている以上は小手先で対処できることは限られており、よほど有力な仮説がなければ、データ量を増やす(つまり対局数を増やしたり、勝敗以外の棋譜データを活用したりする)のが一番ということになります。
これらの問題は、全て時系列データの逐次処理に由来するものです。すでに記録されている一定期間の対局結果を“時系列を無視して”処理する場合には、古典的な統計手法が有効になります(静的レーティングシステムという)。その一つが最尤法です。今回は、この手法について技術的に解説したいと思います。
最初に、歴史的な背景と用語について少し触れておきます。今回の最尤法を用いたレート推定の方法は、Bradley-Terry模型(1952)が最初だと言われています。Bradley-Terry模型の勝率式は、書き換えると、イロレーティングの勝率仮定に一致します。「イロレーティング」という用語は厳密には時系列データを逐次的に処理する手順を含めた総括的なものであり、静的レーティングシステムにおける最尤法による推定模型は「Bradley-Terry模型」というのが正確です。ただし、この用語は専門的であり、一般には通じない可能性が極めて高いため、「イロレーティングを最尤法で」と言っても問題ないかと思います(専門家に怒られないという保証はありませんが)。また、最尤法はベイズ統計で定式化することもできるため、ベイズ統計による静的レーティング(静的ベイジアンELO)であると主張する人もいます。
静的レーティングシステムにおいては、“時系列を無視する”ため、その期間内の全ての対局者のレートが一定であると仮定されており、その全てのレートを同時に推定することになります。これは期間内に大きくレートが変わった者がいる場合には誤差が発生するということを意味しており、特にfloodgateで中身が変わったという場合には注意が必要です(※このような仮定に由来する系統誤差は後述の不確かさの見積もりでは評価不能)。推定時にレート変更の情報があれば、対局者名を変更したり、外れデータとして弾いたりすることもできますが、実際には情報がないことがほとんどであり、対処は困難です。
原理的にレートは相対値であるため、誰かを基準者としてレートの数値を固定し、そこからの相対値を推定します。平均を基準値にしたい場合には、最初に基準者を決めてレートを推定してから、最後に平均が基準値になる様に全体の値をシフトします。基準者は、なるべく中間的な実力で多数の対局者と多く対局している者が向いています。
イロレーティングと同様に、最尤法においてもレートが求まらない対局者が発生することがあります。具体的には、「基準者と対局している者、また、その者と対局している者、また、その者と対局している者、……」という関係集団に含まれていない者、また、関係集団内でも集団内で全勝/全敗の者のレートは算出することができません。推定時には、事前にレート算出が可能であるかを確認して、算出可能者のみの対局に絞って計算する必要があります。
ここでは時系列は考えないため、対局結果は「A対B:何勝何敗」という対局組み合わせ毎のデータリストにまとめることができます。また、ここでは簡単のために引き分けは考えません。引き分けは、取り除くか、0.5勝0.5敗に換算するかというような事前処理が行われているものとします。
最尤法の原理は「データを再現する確率(尤もらしさ)が最大になるように変数(レート)を決める」ということです。ここで、確率を計算する際に仮定/模型が必要になります。仮定/模型の妥当性は、この手法の範囲内では分かりません(※データ量が多い場合には、無作為に選んだ一部のデータを推定に使わずに取っておき、推定結果とそのデータとの整合性から“予言性”を確かめるといった程度の確認なら可能です)。
イロレーティングの勝率仮定(Bradley-Terry模型)においては、確率Pは、
\[P = \prod_{(i, j)} \left[ \frac{1}{1 + 10^{- (R(i) - R(j)) / 400}} \right]^{w(i, j)} \left[ \frac{1}{1 + 10^{- (R(j) - R(i)) / 400}} \right]^{l(i, j)}\]
のように与えられます。ここで、(i, j)は対局組み合わせ、w(i, j)はその対局組み合わせにおけるiの勝ち数、l(i, j)はiの負け数、R(i)はiのレートを表しています。レートの差の部分にさらに相性のレート補正項を入れて(例えば、「R(i) - R(j) + A(i, j)」のように)、補正項のレート変数も含めて、同時に推定するようなこともできますが、変数を増やした分だけ、必要なデータの量も増えますので、豊潤にデータがない限りはお勧めできません。
この確率Pは非常に小さな値になってしまうため、直接的に取り扱わずに自然対数にして取り扱います。すなわち、
\[\ln{P} = - \sum_{(i, j)} \left[ w(i, j) \ln[1 + 10^{- (R(i) - R(j)) / 400}] + l(i, j) \ln[1 + 10^{- (R(j) - R(i)) / 400}] \right]\]
を最大化すればよいわけです。最大値では、変数(レート)に対する偏微分である
\[\frac{\partial{\ln{P}}}{\partial{R(k)}} = \frac{\ln{10}}{400} \sum_{(i, j)} (\delta_{k, i} - \delta_{k, j}) \left[ \frac{w(i, j)}{1 + 10^{(R(i) - R(j)) / 400}} - \frac{l(i, j)}{1 + 10^{(R(j) - R(i)) / 400}} \right]\]
がkに依らずに全て0となります。ここで、クロネッカーのデルタ記号
\[\delta_{i, j} = 0 ~(i = j) ~~\text{or}~~ 1 ~(i \ne j)\]
を使いました。
多変数関数の最大化は、最急降下法や共役勾配法等で、簡単に数値計算することができます。一般的には、非線形連立方程式を解くよりも、最大化の方が簡単です。また、元の関数の符号を反転させれば、最大化は最小化になりますので、最大化と最小化は同じ問題になります。多変数関数の最小化は、拘束条件(ラグランジュ法による正則化)を除けば、ボナンザ式の機械学習と同じですので、結局、最尤法は機械学習と同じことをやればいいということになります。計算の際に必要な初期値は、基準者等に対する勝率から適当に与えれば、よほど変なデータでない限りは上手くいきます。
さて、これで最尤法を用いてレート推定ができるようになったわけですが、推定の結果はどれくらい確か/不確かなのでしょうか?
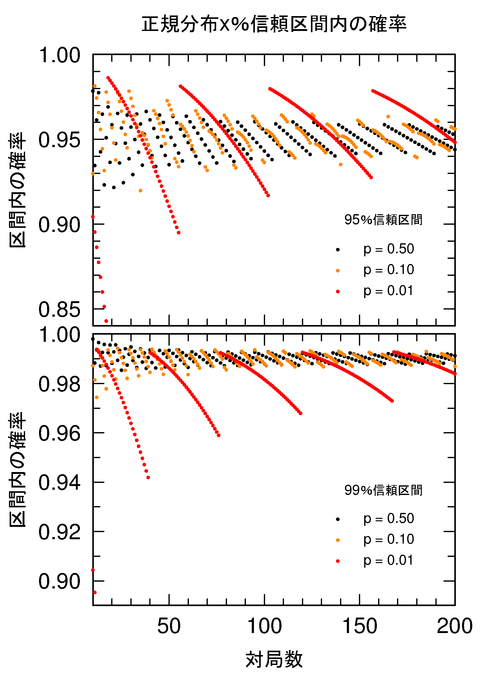
SF的に微妙に異なる平行世界を考えると、棋力(レートの真の値)や対局組み合わせ、対局数が同じであっても、対局結果(w(i, j)とl(i, j)の割合)は確率的にばらつきます。対局結果が異なれば、当然、最尤法によるレートの推定値も変わってきます。つまり、本来はレートの推定値というのは確率的にばらつくものであり、1つの推定値はサイコロを振って偶々出た値の1つに過ぎないと言えます。このような場合、ばらつきの大きさ(不確かさ)を評価して、誤差の目安とします。特に、ばらつきの標準偏差は「標準不確かさ」と呼ばれ、推定値に付記されることが多いものです(※)。
※ 近年の測定論では、推定値(最確値)と標準不確かさを一揃えにして測定値として定義します。系統誤差が無視できる(と仮定する)場合には「標準不確かさ」は「標準誤差」と一致します。
もし仮に、レートの真値が存在し、また、イロレーティングの勝率仮定が正しいとするならば、対局結果をシミュレートすることで、標準不確かさを見積もることができます。ただし、「レートの真値」は分からないものであるため、推定値に近い(誤差が小さい)と仮定して、真値の代わりに推定値で代用します。これは理論的には誤差の高次の項を無視することに対応しています。
最尤法における標準不確かさの評価方法には、計算時に追加する仮定に応じて、いくつかの種類があります(ヘッセ行列の逆行列を用いた方法など)。一般的に、仮定を増やすほど、また、専門的な手法であるほど、計算量が少なくて済みます。
今回の目的においては計算量はあまり重要ではないと思われますので、ここでは、最も仮定が少なく、最も汎用的な(最尤法以外でも使える)手法である「(不確かさ評価における)モンテカルロ法」を紹介します。この手法は、精密測定の分野でも最近よく用いられているものです(模型の造りは異なりますが)。
方法は簡単であり、「レートの真値を推定値で近似して、疑似乱数を用いて対局をシミュレートし、その結果から対応する(平行世界の)推定値を計算することで推定値のばらつきを統計的に評価する」というだけです(つまり“力業”)。大体100~1000回くらい実行すれば、標準不確かさを大よそ見積もることができます。
この方法では、単純計算では推定値の見積もりの100~1000倍の計算量が必要になりますが、実際には、初期値に推定値を与えれば大抵は収束が速いこと、推定値の計算時よりも最大化計算の許容精度をかなり大きく取ってよいこと、並列化が容易であること等から、そこまでの時間はかかりません。
計算上の注意点としては、標準不確かさを評価する際に、元の推定値からの標準偏差ではなく、平均からの標準偏差を見積もるということがあります。一般的に、最尤法の推定値は、分布が偏っている可能性がある(不偏とは限らない)ため、平均とは一致しません。特にイロレーティングの場合には、レートの上限/下限の境界付近で偏りが生じやすくなっています。この偏りを考慮すると、この計算で知りたいのは不確かさ(ばらつきの大きさ)ですので、平均からの標準偏差を見積もる方が適切であるということになります。
以上、今回は、最尤法を用いてレートの推定値と標準不確かさを見積もる方法を解説しました。時系列や逐次処理に拘らなければ、最尤法のような枯れた古典手法が有効になります。目の前の問題の前提を少し変えることで古典手法に落とし込むというのは、レート推定に限らす、一般的に有力な技法です。